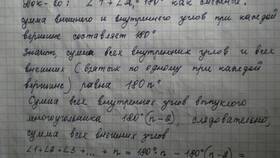В геометрии сумма острых углов зависит от конкретной фигуры и условий задачи. Рассмотрим основные случаи, где встречается понятие острых углов и их суммирование.
Содержание
Сумма острых углов в треугольнике
В любом треугольнике сумма всех углов всегда равна 180°. Для остроугольного треугольника (где все углы меньше 90°) сумма острых углов будет:
- В остроугольном треугольнике - сумма всех трех углов составляет 180°, и каждый из них острый
- В прямоугольном треугольнике - сумма двух острых углов равна 90° (так как третий угол равен 90°)
- В тупоугольном треугольнике - сумма двух острых углов будет меньше 90° (так как тупой угол больше 90°)
Пример расчета
| Тип треугольника | Угол A | Угол B | Угол C | Сумма острых углов |
| Остроугольный | 60° | 70° | 50° | 180° |
| Прямоугольный | 90° | 30° | 60° | 90° |
| Тупоугольный | 100° | 40° | 40° | 80° |
Сумма острых углов в других фигурах
Для многоугольников сумма углов рассчитывается по формуле (n-2)×180°, где n - количество сторон. Количество острых углов может варьироваться:
- В четырехугольнике сумма углов 360°. Если два угла острые (например, по 60°), их сумма будет 120°
- В правильном пятиугольнике все углы равны 108° (тупые), поэтому острых углов нет
- В выпуклых многоугольниках не может быть более трех острых углов
Свойства острых углов
- Острый угол - это угол меньше 90°
- Сумма двух острых углов всегда меньше 180°
- В правильных многоугольниках острых углов не бывает (начиная с пятиугольника)
- В n-угольнике может быть максимум n острых углов при n≤3, и максимум 3 при n>3
Практическое применение
Знание суммы острых углов важно для:
- Решение геометрических задач
- Проектирование архитектурных конструкций
- Компьютерная графика и 3D-моделирование
- Навигационные расчеты